动能定理的应用（动能定理应用技巧）

动能定理的应用（动能定理应用技巧）

前面我们已经对动能和动能定理有了一个比较全面而又粗浅的认识，那从今天开始，我们来看一下动能定理具体的应用技巧有哪些。说白了，这些技巧都是数学意义上的变形。大家仔细体会。

首先我们要有一个基本认识，题目中有速度与位移的关系，一般才会考虑用动能定理。如果出现了速度与时间的关系，我们首先应该考虑的是动量定理。动量定理后续阐述。我们结合一道例题看一看全过程和分段结合如何使用

如图所示，在竖直平面内，粗糙的斜面AB长为2.4m，其下端与光滑的圆弧轨道BCD相切于B，C是最低点，圆心角∠BOC＝37°，D与圆心O等高，圆弧轨道半径R＝1.0 m，现有一个质量为m＝0.2 kg可视为质点的滑块，从D点的正上方h＝1.6 m的E点处自由下落，滑块恰好能运动到A点.（sin37°＝0.6，cos37°＝0.8，g取10 m/s2，计算结果可保留根号）．求：

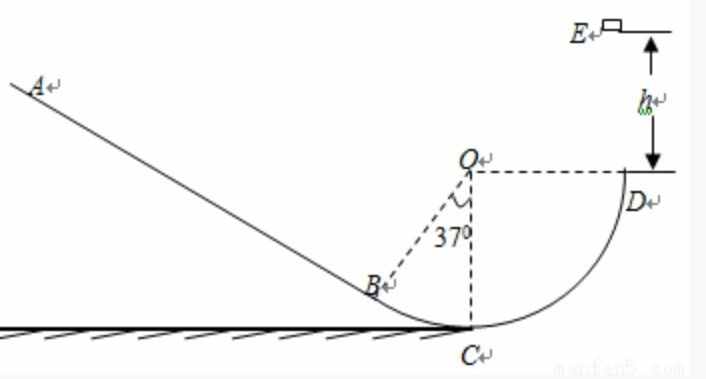
（1）滑块第一次到达B点的速度；

这一问比较简单，但是作为对所学知识的巩固和练习具有很好的锻炼价值。分析，很自然就能想到分段研究，ED为自由落体运动，运动学知识可以知道D的速度v1=根号下(2gh)。动能定理可以知道mgh=(1/2)m(v1的平方)－0，（写零是一个很好的习惯，注意体会）仍然可以得到v1=根号下(2gh)。这恰好验证了动能定理与牛顿第二定律是一致的。DC为光滑圆弧轨道下滑，物体受到的重力是恒力但支持力不管大小如何变，方向一直在变，所以运动学无法求解。又因为是变力很容易就想到用动能定理mgR+0=(1/2)m(v2的平方)－(1/2)m(v1的平方)，v2为C点的速度。同理CB段用动能定理－mgR(1－cos37°)+0=(1/2)m(v3的平方)－(1/2)m(v2的平方)v3为B点的速度。所以B点的速度就求出来了。

不要着急结束，我们再来看下。如果把前面动能定理的三个式子左侧相加等于右侧相加，那么我们就可以得到mgh+mgRcos37°=(1/2)m(v3的平方)－0。是不是利用全过程动能定理就可以更加容易得出结果了呢但是这个容易其实是数学知识的应用。那是不是所有的问题都是全过程动能定理就容易解决呢？我们来看一下第二问。

（2）滑块与斜面AB之间的动摩擦因数；

这次我们先用全过程动能定理，从E点到A点，重力所做的功W1+摩擦力所做的功W2=0－0（再强调一下，不要吝啬多写0）。很容易就能算出摩擦因数为0.5。

还是不要停，再看一下分段，如果看BA段，重力所做的功W3+摩擦力所做的功W2=(1/2)m(v3的平方)－0。也可以解出来。所以，全过程和分段动能定理对同一个问题都可以求解，但是实际情况中，还是大概估计一下哪种方法相对更简单一些。

继续深入，求摩擦因数其实也就是求加速度，这是不是可以说这个模型就是类竖直上抛呢？看透这一点，就可以加深对知识的理解。

（3）滑块在斜面上运动的总路程及总时间．

不要着急去做，我们首先要想一下，为什么有这个问题？这个问题隐藏着什么潜台词？既然问斜面上总路程，那么肯定不是无限大，那是不是说明说明某个时刻，物体停了，速度为零。物体为什么会停，通过分析，不难知道摩擦力做功消耗能量。所以摩擦力的功加上重力的功应该等于动能的变化。摩擦力的功其实我们以前说过的“驴拉磨”模型，重力所做的功只与初末位置有关，那末位置在哪里呢？是最低点吗？这是本题的一个难点。杀手锏，画速度时间图像，我们不难看出，其实物体不是停了，而是恰好无法冲上斜面了，之后在弧BC及其对称位置往返运动了。到目前为止，我们知道了一个关键的信息，物体没有停，而是在B点的速度为零。所以用动能定理不难求出斜面路程了。

那么时间呢？仍然从图像上看，注意两点，一是上下的斜率不一样，因为加速度不一样。二是分段的时间用速度除以加速度就可以知道。三是明显是一个周期函数或者数列。大家可以尝试计算一下。所以图像是物理问题一个很好的辅助工具。如果把弧变成如下的无动能损失的挡板其实也是换汤不换药。