什么是素数（有哪些和素数有关的数学猜想）

素数是所有数字的基础，就如元素周期表中的化学元素一样，化学元素是组成所有化学物质的基础，素数包含了数的所有奥秘，所以数学研究者对素数有着特殊的喜爱。

素数

素数也叫质数，指大于1的自然数中，除了1和它本身外不再有其他因数的自然数，比如2、3、5、7、11、13……。

最初研究素数的是古希腊数学家欧几里得（约公元前330年—前275年），他在《几何原本》中用反证法，对“素数有无穷多个”给出了一个经典的证明方法。

证明思路：

假设存在最大的素数P，那么将已知所有的素数相乘再加1，得到M：

M=2×3×5×7×11×……×P+1，

显然M不可能被已知的任何一个素数整除，所以M有可能是素数，或者存在比P更大但是比M小的素数因子；无论哪种情况，都说明存在比P更大的素数，与假设矛盾，所以素数是无限的。

素数是构成整数的基础，所有整数都可以用素数来表示，如下：

所以素数包含了所有整数的奥秘，整数分解就是破解整数奥秘的途径之一，因为整数分解后只剩下素数因子。

素数的应用

在现实生活中，数的分解是许多网络加密的基础，我们要把两个已知数相乘很容易，但是要把一个大数分解却很难，利用整数的这一非对称特性，密码学家巧妙地设计了加密和解密的数学原理，比如RSA非对称加密算法，就是基于大数分解。

换句话说，一旦出现一种算法能很快地分解一个大数，那么RSA加密方法将失效，但是目前为止还没有出现这样的高效算法。

素数的未解之谜

数学家围绕素数发现了许多规律，其中很多还是猜想，有些历经几百年也没有人能够证明，这些猜想都是数学上的圣杯，谁要是能证明其一，必定名留青史。

（1）哥德巴赫猜想

猜想内容：任何一个大于2的偶数，都可以写成两个素数之和，简称“1+1=2”。

哥德巴赫于1742年提出，如今已经270多年，最好的成果是我国数学家陈景润证明的“1+2”，也就是：任一充分大的偶数，都可以写成一个素数与一个不超过两个素数的乘积之和。

（2）孪生素数猜想

相差2的素数对叫做孪生素数，比如5和7，11和13，该猜想说的是孪生素数有无穷多对。

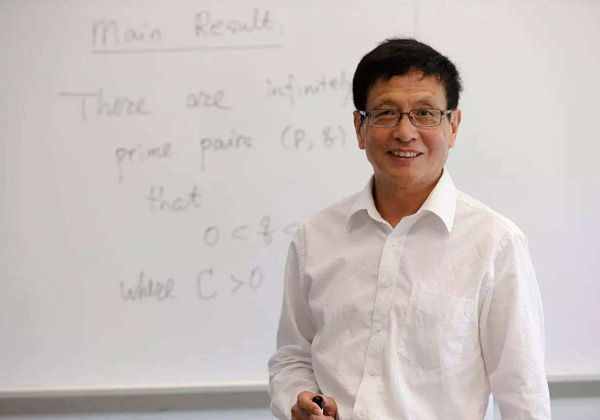
目前最好的成果，是美籍华人数学家张益唐，在2013年提出一种方法，证明存在无穷多个差小于某个数M的素数对，当时张益唐证明了M=7000万的情况，一旦完成M=2就解决了孪生素数猜想，目前M已经被缩小到了200多。

（3）ABC猜想

该猜想描述了三个互素整数a、b、c（满足a+b=c）的素因子之间的关系，是数论中一个非常美妙的猜想，也是一个非常强的数学猜想，一旦ABC猜想被证明，那么证明费马大定理只需要短短五句话。