圆柱（图形与几何---圆柱）

圆柱（图形与几何---圆柱）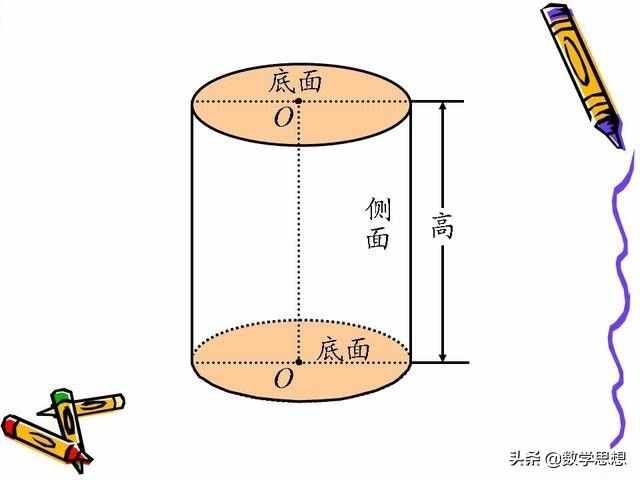

一．概念描述

现代数学：由一个矩形绕其一边旋转一周而成的几何体称为直圆柱或正圆柱，简称圆柱。如下图，

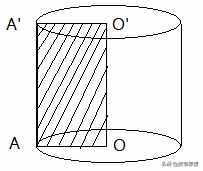
OO’叫作圆柱的旋转轴（简称轴）；矩形中垂直于轴的边OA和O’A’旋转而成的圆面称为圆柱的底面；两个底面间的距离是圆柱的高；矩形中平行于轴的边AA’旋转而成的圆柱面称为圆柱的侧面；侧面上平行于AA’的线段都叫作圆柱的母线。

小学数学：小学数学教材没有直接定义圆柱，主要是通过几何图形建立圆柱的表象，从圆柱的特征把握圆柱。

二．概念解读

(1)圆柱的认识历程

人类在圆柱的研究历程中主要有以下三个重要的标志：

①古希腊时期，阿基米德在《球和圆柱》中阐述了他对圆柱侧面积的研究结果：任何直圆柱曲面的面积，等于一个圆的面积，这个圆的半径是圆柱的高和底面直径之间的比例中项即，r的平方=hd。

②公元500年左右，祖暅（祖冲之之子）在《缀术》中这样记载“幂势既同，则积不容异”，被后人称之为“祖暅原理”。 这也就是“等积原理”，意思是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等。

③16世纪下半叶，德国科学家开普勒在《酒桶的新立体几何》中将酒桶看成由无数的圆薄片累计而成，进而求其体积，这是积分学的萌芽

(2)圆柱的主要特征

圆柱主要有以下特征。

①圆柱的两个底面是相等的圆，它们所在的平面平行。

②圆柱的母线互相平行，且都等于圆柱的高，都垂直于圆柱的两个底面。

③圆柱的轴过两底面的圆心，并且垂直于两底面，它的长等于圆柱的高。

④圆柱的轴截面是一个矩形，它的一组对边是圆柱的两条母线，另一组对边是圆柱底面圆的直径。

⑤平行于底面的截面是与底面相等的圆。

⑥圆柱的侧面可以展开在一个平面上。

三．教学建议

(1)圆柱的教学线索

圆柱的教学可以从以下三条主线和七个维度来组织教学。

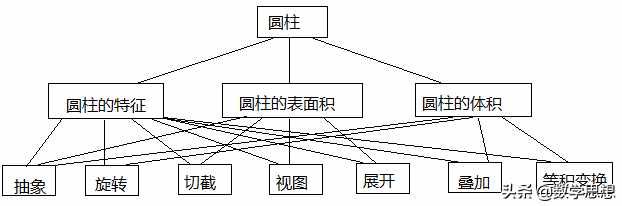
(2)圆柱的教学建没

①动静结合，充分认识圆柱特征。