c42怎么算(排列里面C和A具体怎么计算)

小伙伴们，作为公考中的“常青树”、国考中的必考题，排列组合是很“恶心”的一类题目。你会说，这不是高中就没学好的玩意吗？是的，这么难，有没有信心跟着老师，拿下它？!

先简单介绍一下这个章节。

排列组合是从给定元素中有要求的取出指定的数目，研究这一过程中可能出现的情况数(好枯燥的定义)。其实老师是想告诉大家如何认清题目特征——它基本会以“有多少种情况”、“多少种可能性”、“多少种方案/方式/方法”做为最后的问题。

【例】一张节目表上原有3个节目，如果保持这3个节目的相对顺序不变，再添加进去2个新节目，有多少种安排方法？

a.20b.12c.6d.4

其次我们来看一下最基础的计算方法，也是基本原理。

1) 分类与分步

分类即是加法原理，要求是每种方法都能独立完成任务。分步——乘法原理，此时每种方法不能独立完成任务，任务分为几个步骤，需要逐步完成。

举个例子，沈阳的小华和小图打算十一结伴去成都旅游，出发日期定为9月30日。当天出发的有12班飞机和2趟火车。问两人有多少种选择去成都？

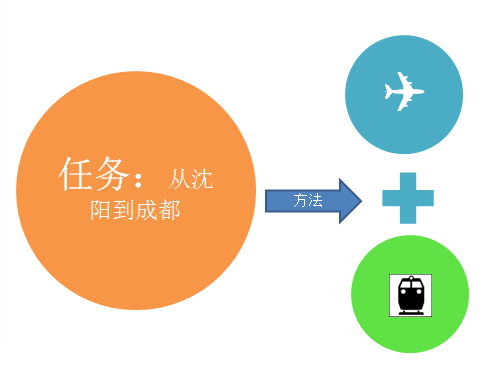
我们发现，12班飞机中的每一班都能让小华和小图到达成都，同样2趟火车中的每一趟也都能完成任务，它们彼此独立、地位相同，都能满足2个人，因此计算情况总数要用加法：12 2=14。

再看一个例子：为奖励优秀教师，华图教育与旅行社沟通想制订欧洲深度游旅行线路。考虑到各个因素，首站有3个国家可选：法国、意大利、瑞士，第二站有4个国家可选：希腊、英国、西班牙、冰岛。若每站只选择1个国家，一共有多少种不同的线路？

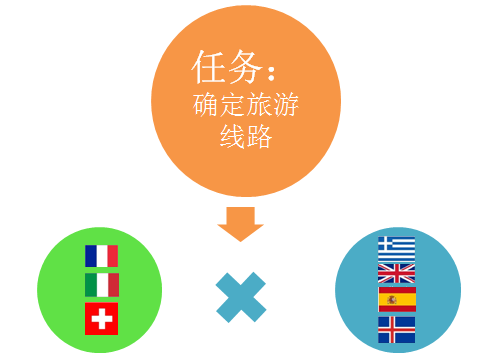
完成旅游路线的制订需要两个步骤：确定第一站国家和确定第二站国家，其中单独的任意一项都不能完成总任务，因此这里我们需要用乘法：34=12。或者也可以简单去想，为什么这里要用乘号？!第一站有3个国家，但仔细考虑，这其中的每一个国家都会对应第二站的4种情况，所以列式要用乘号连接。

1) a(计算顺序)与c(不计顺序)。

好了，今天给小伙伴们介绍的都是排列组合中最基础的知识点，是一切特效技巧的基础。至于排列组合藐视一切考题、见招拆招的“五大神功”，请我们，老师稍后奉上哟!当然，对于今天的知识点，我们还是要留两道国考题练手，答案解析还是老规矩，在华图砖题库搜索吧~

【练习】把4个不同的球放入4个不同的盒子中，每个盒子最多放一个球，有多少种放法？

a.24b.4c.12d.10

【练习】林辉在自助餐店就餐，他准备挑选三种肉类中的一种肉类，四种蔬菜中的二种不同蔬菜，以及四种点心中的一种点心。若不考虑食物的挑选次序，则他可以有多少种不同的选择方法？

a.4b.24c.72d.144

华图教育祝各位考生一举成“公”！

北京华图是您报考国家公务员考试的得力帮手，我们将为您提供及时的招考信息、精品的辅导课程以及贴心的备考服务。